Why doesn't QSpice support Series Inductance in the cpacitor model?

[Mathias]

Is there a reason, why Qspice has no LSER or equivalent attribute in it’s capacitor model?
Granted, it’s trivial to add by hand, but based on this logic, why add an ESR parameter?
Or am I missing something? I’ve checked the “pertinent help file” for capacitances for any mention of inductance, but didn’t find anything.

[KSKelvin]

Mike explained why ESL (equivalent series inductance) or LSER (series inductance) not implemented in Qspice. You won’t find series inductance parameter in Pspice, Hspice, NGspice, TINA-TI etc… but only in LTspice.

ESL in capacitor model

For any type of film capacitor, it is more of a distributed Rser/Rpar/Lser/Cpar network. Poorly described with a single lumped series L. For a ceramic capacitor, a series inductance can be a more viable representation, but usually adds no accuracy to the simulation since connecting inductance often dominates. It was a mistake to support Lser as a part of a capacitor in LTspice. It did much more harm than good. Anyway, below would be a viable equivalent schematic of a film capacitor in lump…

Parasitic inductance of passive components (LSER)

I did not implement Lser for capacitors because it usually caused more harm than good. A series inductance is not a great way to model the internal inductance of a capacitor. For foil capacitors, you really need a ladder of series R & L driving a distributed capacitance, though I’ve been able to match the complex impedance within a few degrees over several decades of frequency with just two lumps. For ceramic capacitors, modeling their internal inductance is not really meaningful without mode…

[daddyzaur]

In addition to the answers you can find already here in the forum, you should check manufacturers like KEMET, Kyocera AVX, TDK to mention a few. They already understood the big picture with oversimplified capacitor models, and they will generate usually through an online tool the best fit capacitor model for your particular need, taking into account your application. Yow can combine all techniques and create a monster capacitor model, but most of the time is a futile exercise. You’re the one that should understand what you need, what a capacitor is, and what is important in your circuit. Here are some examples, starting with a model from KEMET.

*defined as subcircuit
.SUBCKT C2220X106K5RACAUTO n1 n2
* Temp = 25°C, Bias = 0VDC, Center Frequency = 250000 Hz
* 10µF, X7R, KEMET
R1 3 4 0.00424927928611263
R2 2 5 0.400000005960464
R3 n1 n2 100000000
L1 n1 2 5.99500005193931E-11
L2 2 3 1.13905000986847E-09
C1 4 n2 {mc(9.21995707975176u,0.362)}  ;default mc expression
C2 5 n2 1.25E-12
.ENDS C2220X106K5RACAUTO

You can use a capacitor model that accounts for the working voltage:
How to Use LTspice Simulations to Account for the Effect of Voltage Dependence | Analog Devices

If all you need is some basic ESR you can use a model like this one, somehow fit for a Monte Carlo (you can overcomplicate this one to the content of your hearth, mixing and matching all of the above):

*$defined as subcircuit
.SUBCKT MonteCarloCap 1 2 PARAMS:
+ C=1uF TOL=0.2 F=250k DF=0.025 ESR={DF/2/pi/F/C} ;default TOL 0.2 means 20% (tolerance 10% plus aging 10%)
C1 1 3 {mc({C},{TOL})} ;tolerance with aging
R1 3 2 {ESR}
.ENDS MonteCarloCap

Funny thing as a side note, if you add in your model a comment starting with [*$defined] instead of [*defined] it is changing the formatting in something more colorful. Looks like $ and some keywords like “default” are acting as formatting modifiers.

[KSKelvin]

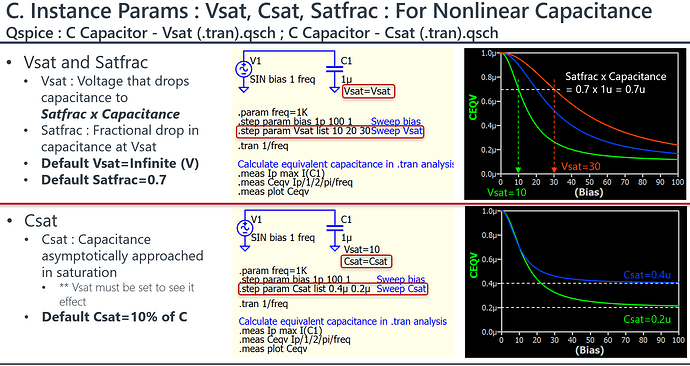
For your info, Qspice offers Vsat, Csat and Satfrac to help model nonlinear voltage dependent capacitor.

[daddyzaur]

Thanks, I was not aware. I still have a long way to jump ship from LTspice to QSPICE, but I am already in mid-air; no way I can stop now: it would be suicide. Man, there are so many improvements, a whole world of options never before available for hardware heads like myself. Thank you guys for your support on the forum, and an mountain of gratitude to @Engelhardt for his work!

[bordodynov]

When modeling in LTspice and using capacitors from Wurth Elektronik, I force the parasitic inductance to zero.

[lpoma]

@Mathias ,

Although QSpice doesn’t support series inductances in the cap model, you can add your own L in series to the cap. This should be an exact equivalent to the sim.

In fact, you can create your own hierarchical symbol with the series L embedded. That way, you can drop this symbol into your schematic as multiple instances.

Len

[glaberson]

LRC models can be very accurate representations of real capacitors. The problem is that the series inductance can cause convergence problems in certain circuits, especially SMPS. In LC filters, they can be very accurate and still converge.

Using the more complex manufacturers’ models in SMPS doesn’t usually solve the problem, because the SPICE models were created without the inductance. There is good reason to include the inductance because it causes the high harmonics of the switching frequency to pass through the output filter. Sometimes it is possible to use an LRC cap model and add a smaller cap in parallel with the LRC model to aid in convergence.