power_example.qsch (4.7 KB)
How is the power dissipated in V1 calculated in Qspice? The value I get does not match the value obtained by get the Ave(P(Vin)). 1) V1rmsIrmscos(phi), after determining the phase difference between V and I, and 2) Vinpk4/pi/sqrtIrms*cos(phi), and neither gets me the same answer that P(v1) gets.
The time-average of voltage times current
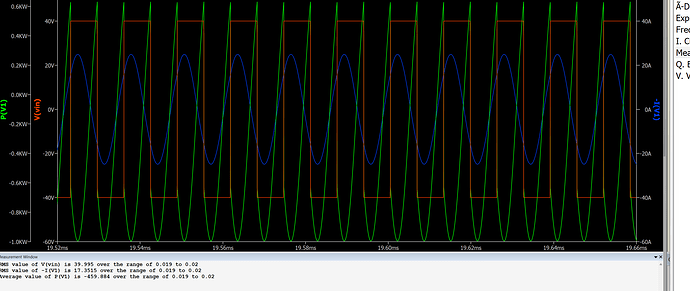
Average value of V(vin)*I(V1) is -459.884 over the range of 0.019 to 0.02
that is, multiply V*I at every time-step, and average that over time.
When the waveforms are significantly different from sinewaves, I do not know any way to compute a phase angle φ from the relative phases of the waveforms. One has to find the ratio of the time-average described above, and find the angle that gives a power factor cos(φ) that reproduces the time average. [edit: … or better, talk about a ‘power factor’ rather than any phase angles.]
thank you. I thought I could measure the distance between the zero crossings of the voltage and current waveforms : delta-T/period360 would give me the phase angle… But sure enough, averaging the instantaenous power gives the right answer. thank you.
So, efficiency would then just be Po /Pin = Iorms^2R1/avg(V1*I1)?
I can’t confirm your proposed way to figure efficiency, because I don’t know how electrical engineers define the term ‘efficiency’.
It looks reasonable to me. RMS(I_o)^2 seems to say the square of the square-root of the mean of the square of the current, which is a roundabout way to get to mean square current.
Power is a topic that people easy get confuse. Get to the basic, real power is the integration of voltage * current over a period of time and divided by that time difference, therefore, avg(V*I) can give you real power, in regardless of waveform.
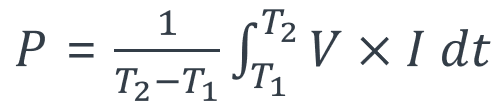
In AC analysis (which assume waveform repeat forever), RMS is used, as a quick method to calculate power from voltage (rms) and current (rms), where Power = Vrms * Irms. But in this equation, it assume voltage and current are in same phase, and same frequency (and only one frequency).
For different phase, they introduce you cos(theta) as power factor, and you can get the real power by multiplying phase difference as cos(theta).
But how about different shape? They introduce you distortion factor (relates to total harmonic distortion THD). Physically, you can understand that, only same frequency voltage and current multiple together can generate that real power. Therefore, you have to take Fourier transform for the waveform and take Vrms*Irms*cos(theta) for each frequencies and sum them up as real power.
What worst is that, if you are not calculating repeating waveform in time domain, it possibly no meaning in rms voltage and current in power calculation.
In short, in power calculation, rms function is only used in voltage and current to help calculating power, and I cannot recall a meaningful way for rms function in power.
And if you are handling non-sinusoidal waveform, possibly the best way is just go to the basic formula - avg(V*I)
In your case,
if V1 is input power : V(vin)*I(V1) , calculate its average result
if R1 is output load : V(vout)*I(R1), calculate its average result