Hello Qorvo community! : ) In re: QM35825 Dev Kit (in a one anchor paradigm only!)
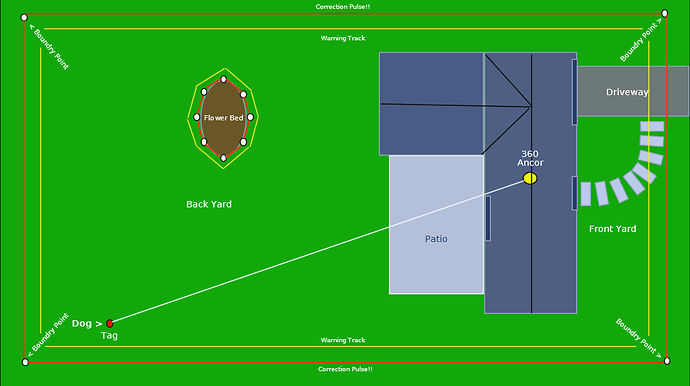
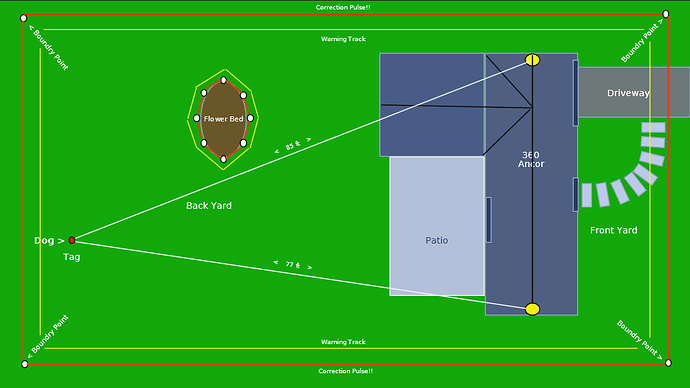
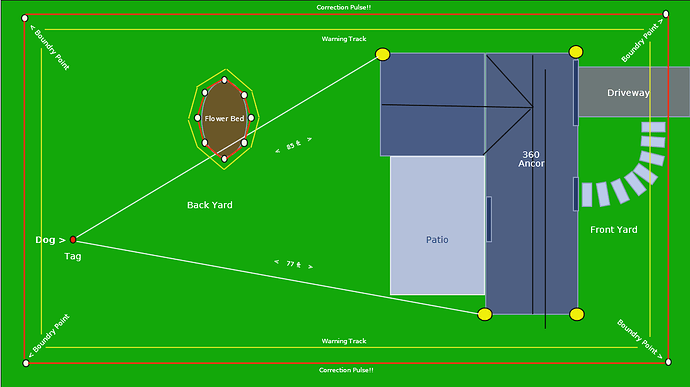
Early thoughts to reduce the inherent "+/- 2 degree uncertainty band (A to B) in the tag’s (red dot) location (see pic).
In a 100ft distance from the anchor (white dot) to the tag … distance is accurate to within +/- 4 inches (perfect for my application!).
… but the “left to right” angular position (A to B) could be anywhere within the uncertainty band of +/- 2.5 feet! : (
Please note: I’m day one with UWB (I don’t even have my evaluation kit as of yet!) : )
My early laymen’s assumptions and thoughts:
In an apparent circular scanning paradigm (UWB phased array) I can locate the tag, but with a +/- 2.5 foot uncertainty of its angular “left or right” (A to B) position.
My thoughts : (Hypothetical with some easy “plug in” numbers)
Lets say the UWB phased array scans this entire 360 circumference in one second.
When it finds a “tag” … I stop this scan dead immediately. The tag has been found in this particular 2 degree angular scan segment , but without an exact angular point! (it could really be anywhere within this uncertainty band).
At this point, I instruct the normal 360 scan rate clock to increase by 100 times! … this accelerated scan rate goes from, lets say, 4 clock cycles residing within this “A to B” segment span … to 100 clock cycles within this same “A to B” distance.
My algorithm then simply counts the clock cycles until the tag no longer presents itself in this fast scan.
ie:
1 clock cycle = tag is located at “A”
thru
50 clock cycles = tag is located at the “center” of this uncertainty band
thru
99 clock cycles = tag is located at “B”
The algorithm would then output the tags true angular position +/- 4 inches!
Basically,
Scan (search) 360 degrees at normal clock speed, stop scan when it detects a tag, Fast scan just this fixed uncertainty area +/- , counting the fast scan clocks until tag stops responding to the scan inquiries.
… thoughts on this?
Thank-you!